
Περιεχόμενο
- Ο νόμος του Zipf εξήγησε
- Βασικό πείραμα
- Ο νόμος του Zipf στις αγορές ατμού
- Τι μπορούμε να μάθουμε για το Steam;
- Συμπεράσματα
Πριν από λίγο καιρό ένας φίλος μου πρότεινε να παρακολουθώ βίντεο του Vsauces σχετικά με το νόμο του Zipf, την αρχή του Pareto και τις μυστηριώδεις εμφανίσεις τους γύρω μας. Εδώ είναι λίγο teaser να κερδίσει την προσοχή σας - το 80% όλων των ανθρώπων ζουν στο 20% των πιο δημοφιλείς πόλεις? Το 80% του συνόλου της γης ανήκει στο 20% των πλουσιότερων ιδιοκτητών. Το 80% του συνόλου των σκουπιδιών είναι στους 20% πιο τραχιά δρόμους - όπως προβλέπεται από τον νόμο του Zipf και από την αρχή του Paretos.
Οχι αρκετά? Λοιπόν, όπως ανακάλυψα χθες, η τρύπα του κουνελιού δεν σταματά εκεί ... Γεμάτη σκεπτικισμό, αποφάσισα να δω πόσο χρόνο περνούν οι άνθρωποι παίζοντας παιχνίδια Steam ... Λοιπόν. Το 80% του χρόνου των ανθρώπων δαπανάται παίζοντας το 20% των πιο δημοφιλών παιχνιδιών ... Ενδιαφέρουσες; Λοιπόν, διαβάστε, υπάρχουν περισσότερα για αυτή την ιστορία.
Το ρολόι σε πάνω από 20 λεπτά, η προσπάθεια του Vsauces είναι τρομερή και εξηγεί πολλά από τα μεγάλα πράγματα για το Zipf, ωστόσο είναι πολύ ντροπαλός που μας δείχνει τον κεντρικό μηχανισμό που πιστεύεται ευρέως ότι συμβάλλει στον λόγο για τον οποίο ο Zipf λειτουργεί όπως κάνει. Έτσι πριν συνεχίσουμε θα ήθελα να το εξηγήσω σύντομα.
Ο νόμος του Zipf εξήγησε
Υπάρχουν διάφοροι εννοιολογικοί τρόποι για να εξηγήσουμε τη διαίσθηση πίσω από την αρχή 20/80. Το καλύτερο παράδειγμα, κατά τη γνώμη μου, είναι το ένα για τους κρατήρες της Σελήνης.
Βασικό πείραμα
Έτσι, φανταστείτε αν θέλετε, ότι υπάρχει μια ανέγγιχτη Σελήνη - μια τέλεια λεία επιφάνεια. Τώρα, πείτε ότι υπάρχουν μερικά τυχαία μεγέθους αστεροειδείς που χτύπησαν το φεγγάρι. Όταν ο πρώτος αστεροειδής προσγειώνεται, αφήνει έναν κρατήρα. Τώρα άλλο ένα χτυπά, αφήνοντας έναν κρατήρα αλλού. Κάθε κρατήρας είναι μέρος της συνολικής επιφάνειας, επομένως υπάρχει η πιθανότητα ο επόμενος τυχαίος αστεροειδής να πληγεί κοντά σε έναν υπάρχοντα κρατήρα και να ενωθεί με αυτόν, σχηματίζοντας μια ομάδα. Η πιθανότητα ενός νέου αστεροειδούς να χτυπήσει έναν δεδομένο κρατήρα είναι τότε ανάλογος προς τα υπάρχοντα μεγέθη των κρατήρων και των αστεροειδών. Αυτό σημαίνει ότι ο επόμενος τυχαίος αστεροειδής είναι πιο πιθανό να ενταχθεί στη μεγαλύτερη υπάρχουσα ομάδα, καθιστώντας την ακόμη μεγαλύτερη. Ένα είδος αθροιστικής διαδικασίας, που στη συνέχεια δημιουργεί ένα πλούσιο-get-πλουσιότερο φτωχό-get-lonelier μηχανισμό.
Έχετε αυτό κατά νου, γιατί αυτό θεωρείται ότι είναι η γενική εξήγηση για το "γιατί" ο νόμος Zipfs λειτουργεί με τέτοια μυστηριώδη καθολικότητα. Το παράδειγμα του αστεροειδούς είναι αρκετά απλό, αλλά το ερώτημα είναι τι θα συμβεί σε πολλές επαναλήψεις
Λίγο μπερδεμένο;
Λοιπόν, έκανα ένα gif να οδηγώ αυτό το αρχικό σημείο στο σπίτι. Σημείωση! το γράφημα θα συζητηθεί αργότερα, απλώς δοκιμάστε να απεικονίσετε το πείραμα.

Αν παρατηρήσουμε την πραγματική Σελήνη, αποδεικνύεται ότι, καθώς η ποσότητα των αστεροειδών αυξάνεται σε μεγάλες ποσότητες, οι διαμέτρους του κρατήρα αυξάνονται έτσι ώστε το 20% των μεγαλύτερων κρατήρων να προσεγγίσει το 80% της συνολικής επιφάνειας.
Έτσι, καθώς πηγαίνουμε σε περισσότερους αστεροειδείς, η διανομή των δημοφιλέστερων σε λιγότερο δημοφιλείς ομάδες προσεγγίζει ένα είδος "ιδανικής διανομής" με αυτήν την ιδιοκτησία 20/80 - μια διανομή Pareto. Εάν κάνετε τα μαθηματικά, αποδεικνύεται ότι (γενικά), αν η μεγαλύτερη ομάδα έχει μέγεθος Ν, η δεύτερη μεγαλύτερη ομάδα είναι γύρω στο μέγεθος N / 2, το τρίτο N / 3 και ούτω καθεξής και ούτω καθεξής. Αυτό ονομάζεται νόμος του Zipf. Το περίεργο πράγμα είναι ο νόμος του Zipf και η διανομή του Pareto για ένα εκπληκτικό ποσό στοιχείων (αστεροειδείς) και ομάδες (ομάδες κλερίων). Φυσικά, υπάρχουν λοξές και τυχαίες διαταραχές, αλλά η γενική τάση είναι αναμφισβήτητη.
Ελπίζω να μπορείτε να δείτε πώς οι αστεροειδείς είναι πιο πιθανό να χτυπήσουν μεγάλους κρατήρες στη Σελήνη συνδέοντας τις πόλεις με τις πιο ελκυστικές, αν υπάρχουν ήδη περισσότεροι άνθρωποι που ζουν σε αυτές. Ωστόσο, πρέπει να συνειδητοποιήσουμε ότι οι πόλεις απέχουν πολύ από τις μοναδικές "ομάδες" που συμπεριφέρονται σύμφωνα με το Zipf.
Ακολουθούν ορισμένα παραδείγματα από την έρευνα του Mark Newmans σχετικά με τις διανομές του Pareto. Σημείωση! Τα γραφήματα είναι σε κλίμακα λογαριθμικής καταγραφής, η οποία εξομαλύνει την υπερβολική μορφή των καμπυλών, παρουσιάζοντας σχεδόν γραμμική σχέση.
Αρχικό y = aX ^ (- b)
Μητρώα και των δύο πλευρών => log y = log a - b log X
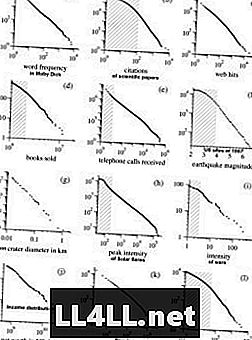
Είναι ενδιαφέρον ότι η ίδια τάση εμφανίζεται επίσης από θρησκευτικές λατρείες ... Η κοινή ιδιοκτησία των περισσότερων από αυτά τα φαινόμενα είναι απλά αυτή η τάση "μεγάλων ομάδων-μεγαλώνουν". Ο νόμος του Zipf είναι συνεχής στους μηχανισμούς, όπου οι προτιμήσεις των στοιχείων συνδέονται θετικά με το μέγεθος των ομάδων (δηλαδή, όσο μεγαλύτερη είναι η ομάδα, τόσο πιο πιθανή θα είναι η ανάπτυξή του). Αυτός είναι ο λόγος για τον οποίο μου αρέσει να σκέφτομαι τις ομάδες ως ομάδες και στοιχεία όπως οι συστάδες.
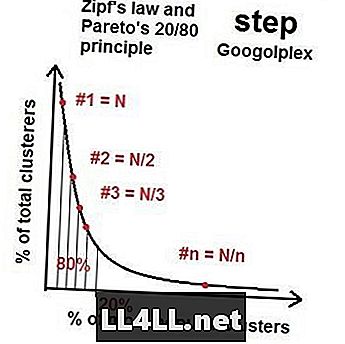
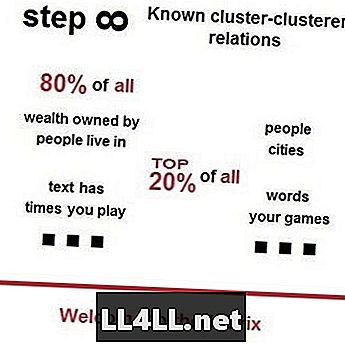
Ο νόμος του Zipf στις αγορές ατμού
Είναι ύποπτος από τον τελευταίο; Εδώ είναι ο χρόνος που ξοδεύουν οι άνθρωποι στα πιο δημοφιλή παιχνίδια του Steam .. Δεδομένα από το SteamSpy.
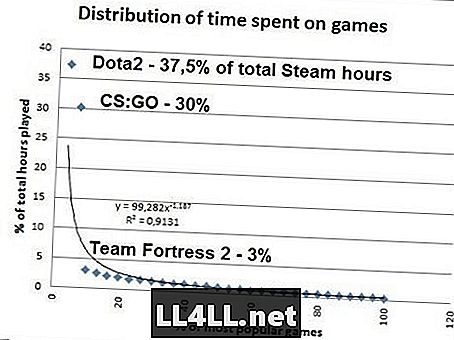
Εάν κάνετε τα μαθηματικά, αποδεικνύεται ότι το 20% των δημοφιλέστερων παιχνιδιών Steam αντιπροσωπεύει το 80% του συνολικού ποσού του παιχνιδιού, οπότε το μυστήριο Pareto 20/80 λειτουργεί σαν γοητεία εδώ ... Πρέπει κανείς να παρατηρήσει, Το Zipf είναι αλήθεια, CS: GO πρέπει να αντιπροσωπεύει το 37,5% / 2 = 18,8% του συνολικού χρόνου αντί για το επιβλητικό 30%. Αλλά εκτός από αυτό το outlier (STOP PLAYING CS: GO), η διανομή τύπου Zipf είναι σαφώς εκεί.
Εδώ είναι το ποσό των αντιτύπων που πωλούνται για τα πιο δημοφιλή παιχνίδια.
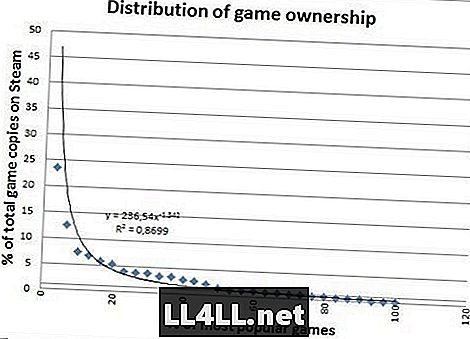
Φαίνεται πολύ ωραιότερο eh; Τα αντίγραφα που πωλούνται δεν έχουν μεγάλες απολήξεις, ώστε να ταιριάζουν πολύ καλά, κάτι που αποτελεί αξιοσημείωτη διαφορά. Ωστόσο, υπάρχει κάτι πιο ενδιαφέρον να συμπεράνει κανείς από τις διαφορές των δύο τελευταίων γραφικών παραστάσεων.
Βλέπετε πώς η "ουρά" προς τα δεξιά είναι κάπως λίπος στο δεύτερο γράφημα; Λοιπόν, με απλά λόγια, αυτό μας λέει ότι τα "σχετικά δημοφιλή" παιχνίδια είναι στην πραγματικότητα πολύ πιο δημοφιλή από ό, τι στην προηγούμενη πλοκή.
Στην πραγματικότητα, αποδεικνύεται ότι το 20% των δημοφιλέστερων παιχνιδιών αντιπροσωπεύει μόνο το 60% των πωλήσεων, έναντι του 80% του παιχνιδιού. Ενδιαφέρων? Σας στοιχηματίζω ότι είναι.
Τι μπορούμε να μάθουμε για το Steam;
Λοιπόν, το γεγονός ότι η δημοτικότητα του παιχνιδιού ακολουθεί τη διανομή Pareto μας λέει ότι πράγματι υπάρχει κάποιο είδος θετικού αποτελέσματος δικτύου, το οποίο κάνει τους παίκτες να επιλέγουν παιχνίδια που ήδη παίζονται από περισσότερους ανθρώπους. Αυτό που μας λέει η διαφορά στο λίπος των ουρών είναι ότι οι χρήστες του Steam είναι πολύ πιο "ομαδοί-τυφλοί", όταν αγοράζουν παιχνίδια από ό, τι όταν παίζουν.
Σκεφτείτε το - όσο περισσότεροι άνθρωποι αγοράζουν παιχνίδια ανεξάρτητα από την "τρέχουσα δημοφιλή γνώμη", τόσο πιο πεπλατυσμένη είναι η διανομή Pareto, καθώς είναι λιγότερο πιθανό για μεγάλα παιχνίδια να αναπτυχθούν περαιτέρω. Εάν κανείς δεν έδωσε ένα ποντίκι για το πόσοι άνθρωποι παίζουν ήδη ένα παιχνίδι και η διαθεσιμότητα όλων των παιχνιδιών ήταν ίδια, τότε θα περίμενε το 20% των πιο δημοφιλών παιχνιδιών να αντιπροσωπεύουν περίπου το 50% των πωλήσεων και του χρόνου παιχνιδιού (π.χ. κανονικά κατανεμημένα).
Συμπεράσματα
Έτσι, υπάρχουν δύο παράγοντες που συμβάλλουν στην κατανομή Pareto στις αγορές ατμού - πόσο καινοτόμοι είναι οι προγραμματιστές (πόσοι νέοι κρατήρες της Σελήνης σχηματίζονται) και πόσο οι παίκτες (αστεροειδείς) εκτιμούν το μέγεθος της τρέχουσας ομάδας, επιλέγοντας ποια ομάδα θα συμμετάσχει . Όπως αποδεικνύεται, οι παίκτες είναι πολύ τυφλοί κατά την αγορά παιχνιδιών, αλλά ακριβώς το αντίθετο όταν τους παίζουν. Cool;
Αν θέλετε να μάθετε περισσότερα σχετικά με τις διανομές νόμου και εξουσίας του Zipf, εδώ είναι μια ωραία διάλεξη. Επιπλέον, φροντίστε να ρίξετε μια ματιά στο χαρτί του Newman!
Εάν θέλετε να διαβάσετε περισσότερα τέτοια πράγματα, σύντομα θα προσπαθήσω να συμμετάσχω σε αυτή την παρατήρηση σε ένα μοντέλο, το οποίο δείχνει ότι τα δημοφιλέστερα παιχνίδια για πολλούς παίκτες έχουν υψηλότερες τιμές (γεγονός που συνδέει την προτίμηση των gamers να ενταχθούν σε ομάδες μεγαλύτερου μεγέθους). Δείτε το άρθρο εδώ. Το άρθρο Piece De Resistance θα προσπαθήσει να ενταχθεί μαζί σε αυτές τις θεωρίες, εξηγώντας πώς τα παιχνίδια για πολλούς παίκτες, τα κοινωνικά δίκτυα και οι πόλεις είναι στην πραγματικότητα όλα τα αντικρουόμενα αγαθά με επιπτώσεις στο δίκτυο (όσο περισσότεροι άνθρωποι καταναλώνουν ένα καλό, τόσο περισσότερο ωφελήσουν μεμονωμένοι καταναλωτές) τους δικαίωσε με αυτή τη ζιφιακή ομίχλη μυστηρίου ...
Μέχρι τότε - απολαύστε τους εαυτούς σας!
P.S. Δημοσιεύστε ένα σχόλιο με μια ιδέα διασκέδασης για μια σχέση 20/80 που νομίζετε ότι μπορεί να είναι αλήθεια.
Ορυχείο είναι:
Το 80% της λαϊκής νοσταλγίας προκαλείται από το 20% των πιο ευχάριστων αναμνήσεών τους (πράγματι αποδεδειγμένο για το ρυθμό που οι άνθρωποι ξεχνούν τις πληροφορίες)
Το 80% της μάζας συγκεντρώνεται στο 20% των μεγαλύτερων διαστημικών αντικειμένων (πράγματι αποδεδειγμένο για τη διανομή της βαρυτικής δύναμης)
Και φυσικά
Το 80% του χάος στην τουαλέτα σας προέρχεται από το 20% του τι τρώτε (δεν υπάρχει καμία ακαδημαϊκή έρευνα για να μιλήσετε)