
Περιεχόμενο
Η γενική προϋπόθεση του κυριολεκτικού πλάσματος στο Επίθεση στον Τιτάνα: Φτερά της Ελευθερίας είναι ότι είναι άνθρωποι διευρυμένοι και ως επί το πλείστον χωρίς νόημα. Μερικοί δεν έχουν δέρμα, καθιστώντας τους πιο φρικιαστικούς, αλλά αυτό δεν είναι το μόνο πράγμα που τους κάνει διαφορετικούς από τους άλλους γίγαντες. Έχουν μια ακόρεστη όρεξη για τον άνθρωπο. Και αυτά τα πλάσματα είναι όλοι οι λόγοι για τους οποίους δημιουργήθηκαν τρία γιγαντιαία τείχη γύρω από την πόλη στην ιστορία του παιχνιδιού. Είναι όλοι οι λόγοι πίσω από το 3D εργαλείο ελιγμών που ανέφερα την περασμένη εβδομάδα. Και αν είμαστε ειλικρινείς με τον εαυτό μας, είναι ο λόγος που μας ενδιαφέρει Επίθεση στον τίτανα franchise στην πρώτη θέση.
Πολλοί άνθρωποι έχουν ήδη μιλήσει για την επιστήμη των γιγάντων και σίγουρα θα το συζητήσω και πάλι γιατί είναι εξαιρετικά σημαντικό να κατανοήσουμε τη φυσική πίσω από τους γίγαντες και γιατί ορισμένα ζώα μεγαλώνουν τόσο ψηλά όσο και γιατί τα άλλα δεν το κάνουν. Ωστόσο, η πραγματική μου πρόθεση κατά τη διάρκεια του άρθρου αυτής της εβδομάδας είναι να απαντήσω σε μια διαφορετική ερώτηση: Πόσο μεγάλο μπορεί να πάρει ρεαλιστικά ο Τιτάνας; Έτσι, για άλλη μια φορά, ας σκεφτούμε την επιστήμη Επίθεση στον Τιτάνα: Φτερά της Ελευθερίας.
Λέει ο Γαλιλαίος
Όλοι έχουμε ακούσει για το Galileo, σωστά. Ο τύπος που κοίταζε πολύ τον ουρανό. Λοιπόν, ήταν γνωστός για περισσότερο από την αστρονομία του. Ήταν στην πραγματικότητα ένας ιδιοφυής μαθηματικός. Επιπλέον, ήταν ένας καταπληκτικός παρατηρητής. Στο βιβλίο του Δύο νέες επιστήμες, μιλάει για δύο πλοία, και τα δύο είναι πανομοιότυπα με κάθε τρόπο. Από το σκελετό στο κατάστρωμα και από το τόξο στην πρύμνη, δεν υπήρχαν διαφορές εκτός από ένα: το ένα είναι το διπλάσιο από το άλλο. Παρατηρεί ότι το μεγαλύτερο σκάφος θα απαιτούσε περισσότερη σκαλωσιά και σταθεροποίηση έτσι ώστε να μην καταρρέει κάτω από το βάρος του.
Αλλά αυτό δεν έχει νόημα; Είναι απλά μεγαλύτερο. θα πρέπει να έχει τις ίδιες φυσικές ιδιότητες με κάτι μικρότερο, σωστά; Δυστυχώς, ο ισχυρισμός αυτός είναι εσφαλμένος. Σε ένα θεμελιώδες επίπεδο, τα άτομα σε κάθε ένα από τα αντικείμενα είναι τα ίδια, αλλά υπάρχουν περισσότερα άτομα στο μεγαλύτερο στοιχείο, αλλά σε πιο πρακτικό επίπεδο, η γεωμετρία αλλάζει με το μεγαλύτερο αντικείμενο.
Φανταστείτε έναν κύβο που είναι 1 cm έως 1 cm, ο όγκος του είναι 1 cm³ ή 1 l και η μάζα του είναι περίπου 1 g εάν γεμίσει με νερό. Πόσο νερό θα κρατούσε ένας κύβος των 10 cm; Εάν σκέφτεστε 10 cm³ ή ακόμα και 100 cm³, θα λάβατε λάθος. Θα κρατούσε 1.000 cm³. Επιπλέον, η μάζα τριπλασιάστηκε αναλογικά σε 1.000 g. Αυτό ονομάζεται νόμος πλατεία-κύβου του Galileo.
Ένας Τιτάνας είναι ανθρώπινη αναλογία, αλλά στέκεται σε ύψος περίπου 15 μ. Εάν ο μέσος άνθρωπος βρίσκεται σε περίπου 1,5 μ. (Δείτε πού πηγαίνω με αυτό;), τότε ο Τιτάνας είναι 10 φορές υψηλότερος. Εάν ολοκληρώσουμε το μέσο βάρος ενός ανθρώπου 1,5 m στα 70 kg. Αυτό σημαίνει ότι ένας γίγαντας με μέγεθος 10 φορές μεγαλύτερο από το ύψος του θα είχε 1.000 φορές τη μάζα, 70.000 κιλά. Αυτό είναι 70 μετρικοί τόνοι. Χωρίς καμία επιπλέον δομή στήριξης, ένας Τιτάνας θα συνθλίβεται με το δικό του βάρος, για να μην αναφέρουμε τη δύναμη που θα χρειαζόταν για να αντλήσει αυτό το πολύ αίμα μέσω του συστήματός του.
Σε μια πλάγια σημείωση, όταν κόβετε ένα Τιτάν στο πίσω μέρος του λαιμού, αναβλύζει αίμα. Αντιλαμβάνεστε ότι αν ο χαρακτήρας σας επρόκειτο να χτυπηθεί με το ρεύμα των σωματικών υγρών, θα ήταν σαν να χτυπάτε με έναν πλήρως ανοιχτό εύκαμπτο σωλήνα πυρκαγιάς.

Ο Γαλιλαίος είπε στο βιβλίο του: "Τέλος, μπορούμε να πούμε ότι για κάθε μηχανή και δομή, τεχνητή ή φυσική, υπάρχει ένα απαραίτητο όριο πέρα από το οποίο ούτε η τέχνη ούτε η φύση μπορούν να περάσουν. γίνεται αντιληπτό, φυσικά, ότι το υλικό είναι το ίδιο και το ποσοστό διατηρείται. "Με άλλα λόγια, υπάρχει ένα δομικό περιορισμό σε όλα. Ποιοι είναι οι περιορισμοί του ανθρώπινου πλαισίου; Πάω να κολλήσω στο πλαίσιο και όχι στο κυκλοφορικό σύστημα ή σε οποιοδήποτε άλλο σύστημα όπως αυτό λόγω του αριθμού των μεταβλητών που εμπλέκονται, αλλά γνωρίζουμε ότι πολλά από αυτά τα όρια είναι πολύ χαμηλότερα από την εσωτερική δομική ακεραιότητα. Ενδεχομένως να συνεργαζόμαστε με το βέλτιστο σενάριο εδώ.
Ο ψηλότερος άνθρωπος που ζούσε ποτέ γεννήθηκε στο Alton, IL, σε μικρή απόσταση από το παιδικό μου σπίτι στο St. Louis. Το όνομά του ήταν ο Robert Wadlow. Στέκεται σε πλήρη 8 πόδια 11 ίντσες (2.7178 μ.). Πάνω από ένα μέτρο υψηλότερο από τον μέσο άνθρωπο. Και παρά το γεγονός ότι ήταν πολύ κοκαλιάρικο, ζύγιζε 220 κιλά, πάνω από τρεις φορές εκείνη ενός μέσου ανθρώπου. Ο Wadlow έπρεπε ακόμη να φορέσει ειδικά τιράντες στα πόδια του για να του δώσει επιπλέον υποστήριξη για τη μάζα του. Δυστυχώς, ο Wadlow πέθανε στα πολύ νεαρά 22 χρόνια λόγω επιπλοκών με το ύψος του.
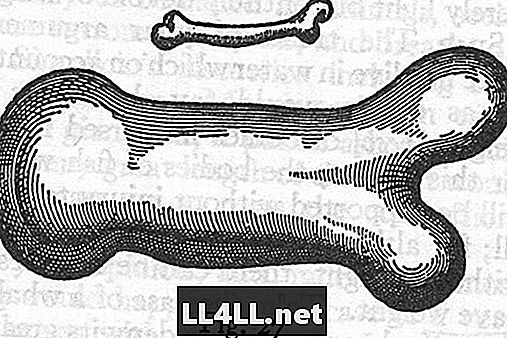
Ο Γαλιλαίος υπολόγισε ότι η δομή των οστών για κάτι που είναι διπλάσιο από το ύψος ενός ανθρώπου θα έπρεπε να είναι περίπου τέσσερις φορές παχύτερο. Έβγαλε ακόμη και μια εικόνα ενός οστού ποδιών. Ωστόσο, εξακολουθούν να υπάρχουν προβλήματα με τη χρήση αυτού σε ένα τιτάνιο όταν εξετάζετε το όριο στρες του οστού γενικά.
Ένα ανθρώπινο οστό έχει την ισχύ περίπου 4.400 MN / m², πράγμα που σημαίνει ότι αν η πίεση πάνω από το κόκκαλο είναι μεγαλύτερη από 4.000 NM, θα συνθλιβεί. Ένας μέσος άνθρωπος ασκεί 55 MN / m² στέκεται ή 110 MN / m² στα οστά του όταν περπατά, δεν είναι κακό. Αλλά ένας Τιτάνας βάρους 70 τόνων θα έβαζε 110.000 MN / m² εάν κάναμε μια απλή αναλογία.
Πραγματικώς, ένας Τιτάνας δεν θα μπορούσε να είναι πολύ μεγαλύτερος από τον Wadlow, περίπου 3 μέτρα, αλλά πού είναι η διασκέδαση σε αυτό; Επιτρέψτε μου να ξέρω τι σκέφτεστε στα σχόλια και επιτρέψτε μου να ξέρω τι συμβαίνει όταν επιστήσατε τα σκατά από αυτό.
